Les grands défis d’aujourd’hui

Imaginez une toile tendue : elle peut être plate comme une feuille de papier, courbe vers l’intérieur comme une sphère, ou courbe vers l’extérieur comme une selle de cheval.

La théorie de la Relativité Générale introduit la courbure de l’espace-temps provoquée par la gravitation (cf la page « Mouvements et gravitation »). Cette courbure « locale » est par exemple mise en évidence par les trajectoires de tout corps ou lumière à proximité d’un corps massique. On peut notamment observer la courbure des rayons lumineux d’une étoile au voisinage d’un trou noir, ou bien l’image d’une galaxie à travers une lentille gravitationnelle.

A l’échelle cosmique globale, cette courbure est étroitement liée à la densité de masse moyenne de l’univers (matière classique/baryonique et matière noire) que l’on caractérise par le « paramètre de densité » Ω. Mais pour tenir compte de l’accélération de l’expansion de l’Univers, il faut également considérer la densité moyenne d’énergie du vide (cf la page « L’énergie du vide« ), caractérisée par la « constante cosmologique » Λ (cf la page « L’expansion de l’univers »).

A l’échelle de l’univers observable, le rayon de courbure Rc est défini par la relation :

avec R_H, le rayon de Hubble :

${\displaystyle R_H=c/H}$ ${\displaystyle \mathrm{avec }}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;"><em>c</em>\; =\; vitesse\; de\; la\; lumière,</span>}}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;">et\; <em>H</em>\; =\; <span\; style="font-family:\; \text{'}Open\; Sans\text{'},\; Arial,\; sans-serif;">constante\; de\; Hubble</span></span>}}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;"><span\; style="font-family:\; \text{'}Open\; Sans\text{'},\; Arial,\; sans-serif;">(rapport\; entre\; la\; distance\; et\; la\; vitesse\; de\; récession\; des\; galaxies)</span></span>}}$

Si l’on fait l’hypothèse, simplificatrice mais largement reconnue par communauté scientifique, et justifiée par les observations récentes, d’une distribution uniforme de la matière et de l’énergie dans l’univers (homogénéité et isotropie), alors il est mathématiquement démontrable que la courbure à l’échelle du cosmos est constante.

A cette échelle, seulement trois types d’univers peuvent être considérés :

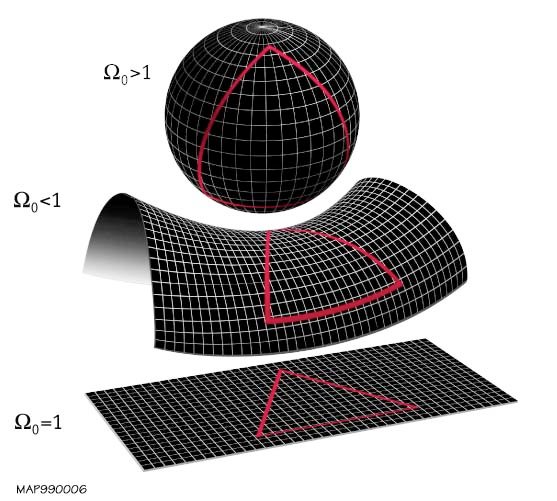
• Univers « plat » : Un univers plat est celui où les géodésiques (les lignes les plus courtes entre deux points, cf la page « Distance et temps« ) sont des lignes droites. Deux géodésiques initialement parallèles ne se rejoignent jamais dans ce type d’univers. Il correspond à une géométrie euclidienne dans laquelle la somme des angles d’un triangle est égale à 180° et dans laquelle le théorème de Pythagore est vérifié (). Sa courbure est alors dite « nulle ». Son paramètre de densité Ω est égal à 1. Attention cependant au terme « plat » : la surface d’une feuille de papier dont on a joint (« identifié ») deux bords opposés (tube) relève bien de la géométrie euclidienne. On « sort » par l’un de ces bords joints en entrant immédiatement par l’autre. Il en est de même pour la surface d’un tore qui correspond à un tube rebouclé sur lui-même.

• Univers sphérique : Dans un tel univers, si on voyage suffisamment loin sur une géodésique (ici des arcs de cercle), on finit par revenir au point de départ. Et deux géodésiques initialement parallèles finissent par se croiser comme deux méridiens terrestres se croisent aux pôles. Il correspond à une géométrie sphérique ou elliptique dans laquelle la somme des angles d’un triangle est supérieure à 180° et la surface de ce triangle est supérieure à celle calculée dans un espace euclidien. Dans ce type d’univers le théorème de Pythagore ne s’applique pas. Sa courbure est dite « positive ». Son paramètre de densité Ω est supérieur à 1. Cet espace fini et sans bord a été l’espace privilégié initialement par Einstein. Un univers sphérique pourrait expliquer quelques énigmes cosmologiques comme les disparités dans les mesures de la constante de Hubble (cf le page « La tension de Hubble« ). Les données du télescope spatial Planck semblent indiquer que la courbure de l’univers serait très légèrement sphérique.

• Univers hyperbolique : Il s’agit d’un univers qui repose sur une géométrie hyperbolique dans lequel les géodésiques divergent, la somme des angles d’un triangle est supérieure à 180° et la surface de ce triangle est inférieure à celle calculée dans un espace euclidien. Le théorème de Pythagore n’est pas vérifié non plus dans ce type d’espace. Sa courbure est dite « négative ». Son paramètre de densité Ω est inférieur à 1.

A l’échelle de l’univers observable, le rayon de courbure Rc est défini par la relation :

avec, R

${\displaystyle R_H=c/H}$ ${\displaystyle \mathrm{avec }}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;"><em>c</em>\; =\; vitesse\; de\; la\; lumière,</span>}}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;">et\; <em>H</em>\; =\; <span\; style="font-family:\; \text{'}Open\; Sans\text{'},\; Arial,\; sans-serif;">constante\; de\; Hubble</span></span>}}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;"><span\; style="font-family:\; \text{'}Open\; Sans\text{'},\; Arial,\; sans-serif;">(rapport\; entre\; la\; distance\; et\; la\; vitesse\; de\; récession\; des\; galaxies)</span></span>}}$

Si l’on fait l’hypothèse, simplificatrice mais largement reconnue par communauté scientifique, et justifiée par les observations récentes, d’une distribution uniforme de la matière et de l’énergie dans l’univers (homogénéité et isotropie), alors il est mathématiquement démontrable que la courbure à l’échelle du cosmos est constante.

A cette échelle, seulement trois types d’univers peuvent être considérés :

• Univers « plat » : Un univers plat est celui où les géodésiques (les lignes les plus courtes entre deux points, cf la page « Distance et temps« ) se propagent en ligne droite. Deux géodésiques initialement parallèles ne se rejoignent jamais dans ce type d’univers. Il correspond à une géométrie euclidienne dans laquelle la somme des angles d’un triangle est égale à 180° et dans laquelle le théorème de Pythagore est vérifié (). Sa courbure est alors dite « nulle ». Son paramètre de densité Ω est égal à 1. Attention cependant au terme « plat »: la surface d’une feuille de papier dont on a joint (« identifié ») deux bords opposés (tube) relève bien de la géométrie euclidienne. On « sort » par l’un de ces bords joints en entrant immédiatement par l’autre. Il en est de même pour la surface d’un tore qui correspond à un tube rebouclé sur lui-même.

• Univers sphérique : Dans un tel univers, si on voyage suffisamment loin sur une géodésique (ici des arcs de cercle), on finit par revenir au point de départ. Et deux géodésiques initialement parallèles finissent par se croiser comme deux méridiens terrestres se croisent aux pôles. Il correspond à une géométrie sphérique ou elliptique dans laquelle la somme des angles d’un triangle est supérieure à 180° et la surface de ce triangle est supérieure à celle calculée dans un espace euclidien. Dans ce type d’univers le théorème de Pythagore ne s’applique pas. Sa courbure est dite « positive ». Son paramètre de densité Ω est supérieur à 1. Cet espace fini et sans bord a été l’espace privilégié initialement par Einstein. Un univers sphérique pourrait expliquer quelques énigmes cosmologiques comme les dispartités dans les mesures de la constante de Hubble. Les données du télescope spatial Planck semblent indiquer que la courbure de l’univers serait sphérique.

• Univers hyperbolique : Il s’agit d’un univers qui repose sur une géométrie hyperbolique dans lequel les géodésiques divergent, la somme des angles d’un triangle est supérieure à 180° et la surface de ce triangle est inférieure à celle calculée dans un espace euclidien. Le théorème de Pythagore n’est pas vérifié non plus dans ce type d’espace. Sa courbure est dite « négative ». Son paramètre de densité Ω est inférieur à 1.

A l’échelle de l’univers observable, le rayon de courbure Rc est défini par la relation :

avec, R

${\displaystyle R_H=c/H}$ ${\displaystyle \mathrm{avec }}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;"><em>c</em>\; =\; vitesse\; de\; la\; lumière,</span>}}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;">et\; <em>H</em>\; =\; <span\; style="font-family:\; \text{'}Open\; Sans\text{'},\; Arial,\; sans-serif;">constante\; de\; Hubble</span></span>}}$ ${\displaystyle \mathrm{<span\; style="font-size:\; 17px;"><span\; style="font-family:\; \text{'}Open\; Sans\text{'},\; Arial,\; sans-serif;">(rapport\; entre\; la\; distance\; et\; la\; vitesse\; de\; récession\; des\; galaxies)</span></span>}}$

Si l’on fait l’hypothèse, simplificatrice mais largement reconnue par communauté scientifique, et justifiée par les observations récentes, d’une distribution uniforme de la matière et de l’énergie dans l’univers (homogénéité et isotropie), alors il est mathématiquement démontrable que la courbure à l’échelle du cosmos est constante.

A cette échelle, seulement trois types d’univers peuvent être considérés :

• Univers « plat » : Un univers plat est celui où les géodésiques (les lignes les plus courtes entre deux points, cf la page « Distance et temps« ) se propagent en ligne droite. Deux géodésiques initialement parallèles ne se rejoignent jamais dans ce type d’univers. Il correspond à une géométrie euclidienne dans laquelle la somme des angles d’un triangle est égale à 180° et dans laquelle le théorème de Pythagore est vérifié (). Sa courbure est alors dite « nulle ». Son paramètre de densité Ω est égal à 1. Attention cependant au terme « plat »: la surface d’une feuille de papier dont on a joint (« identifié ») deux bords opposés (tube) relève bien de la géométrie euclidienne. On « sort » par l’un de ces bords joints en entrant immédiatement par l’autre. Il en est de même pour la surface d’un tore qui correspond à un tube rebouclé sur lui-même.

• Univers sphérique : Dans un tel univers, si on voyage suffisamment loin sur une géodésique (ici des arcs de cercle), on finit par revenir au point de départ. Et deux géodésiques initialement parallèles finissent par se croiser comme deux méridiens terrestres se croisent aux pôles. Il correspond à une géométrie sphérique ou elliptique dans laquelle la somme des angles d’un triangle est supérieure à 180° et la surface de ce triangle est supérieure à celle calculée dans un espace euclidien. Dans ce type d’univers le théorème de Pythagore ne s’applique pas. Sa courbure est dite « positive ». Son paramètre de densité Ω est supérieur à 1. Cet espace fini et sans bord a été l’espace privilégié initialement par Einstein. Un univers sphérique pourrait expliquer quelques énigmes cosmologiques comme les disparités dans les mesures de la constante de Hubble.

• Univers hyperbolique : Il s’agit d’un univers qui repose sur une géométrie hyperbolique dans lequel les géodésiques divergent, la somme des angles d’un triangle est supérieure à 180° et la surface de ce triangle est inférieure à celle calculée dans un espace euclidien. Le théorème de Pythagore n’est pas vérifié non plus dans ce type d’espace. Sa courbure est dite « négative ». Son paramètre de densité Ω est inférieur à 1.

La topologie, en mathématiques, étudie les propriétés d’un objet qui sont préservées par des transformations continues. Elle ne s’intéresse pas spécifiquement aux mesures de l’espace, mais à sa forme. En cosmologie, la topologie de l’univers concerne sa forme globale, au-delà de sa courbure.

Plusieurs topologies d’espace-temps sont envisageables, de la plus simple, un univers purement euclidien, infini et sans bord (la feuille de papier plane qui s’étend à l’infini dans toutes les directions), aux plus complexes, avec des « trous », des « torsions » ou encore des « duplications » d’espace dans des univers « multi-connexes ». Par exemple, l’univers pourrait avoir la forme d’un tore, d’un ruban de Möbius, d’une bouteille de Klein ou d’un dodécaèdre de Poincaré. Ces topologies exotiques pourraient expliquer certains phénomènes observés, comme la présence de structures récurrentes dans la distribution des galaxies.

Dans chacune des trois familles de courbure globale vues ci-dessus (euclidienne, sphérique, hyperbolique) les mathématiciens identifient des variantes topologiques. Par exemple, ils démontrent qu’il existe 18 topologies possibles à trois dimensions, correspondant à un univers euclidien.

Il est à noter que dans le standard de la cosmologie, le modèle du Big Bang prévoit que la topologie de l’univers est fixée dès l’origine et ne peut évoluer au cours des phases d’inflation et d’expansion qui ont suivi.

De nombreuses questions se posent lorsque l’on parle de forme de l’univers. Mais la première est : de quel univers parle-t-on ? Le seul univers qui nous est accessible depuis la Terre à travers les tout derniers instruments sophistiqués est l’univers dit observable, noté Univers, c’est-à-dire la portion de l’univers que nous pouvons « voir » grâce aux photons, et depuis peu grâce aux ondes gravitationnelles, qui nous parviennent du fin fond du cosmos. En raison de la vitesse finie de la lumière, cet univers observable est nécessairement fini. Il correspond à une sphère dont nous serions le centre et qui aurait pour rayon la distance parcourue par la lumière depuis la Big Bang, c’est à dire environ 46,5 milliards d’années-lumière. Cette taille étonnante est due à l’expansion de l’Univers depuis son « origine », il y a 17,8 milliards d’années (cf la page « L’expansion de l’univers »). Au-delà de cette limite, la lumière n’a pas eu le temps de nous atteindre, rendant cette région inaccessible à nos observations directes actuelles.

Un univers fini ou infini ?

Quelle que soit sa courbure et sa topologie, le cosmos dans son ensemble pourrait largement dépasser la taille de l’univers observable. Mais même dans ce cas il pourrait être fini, comme une sphère de rayon supérieur 46,5 milliards d’années-lumière.

A noter également qu’alors qu’un univers sphérique (par exemple la surface d’une sphère, si l’on considère uniquement deux dimensions) est nécessairement fini, la finitude des deux autres types d’espace (euclidien ou hyperbolique) dépend de leur topologie. Ils sont généralement infinis dans leurs configurations les plus simples.

Remarquons aussi qu’un univers peut être fini mais sans bord. C’est par exemple le cas de la surface d’une sphère ou d’un tore.

Un univers mono-connexe ou multi-connexe ?

Un univers connexe est un univers dans lequel on peut aller d’un point à un autre sans discontinuité. 

Un univers connexe est dit mono-connexe si toute courbe, y compris boucle, peut être réduite à un point. Dans le cas contraire, l’univers est multi-connexe.

Une feuille de papier ou la surface d’une sphère sont les exemples les plus simples d’un univers mono-connexe. Alors qu’un univers possédant un trou, comme la surface d’un tore par exemple, est multi-connexe, une trajectoire fermée circulaire autour du trou ne pouvant être réduite en un point.

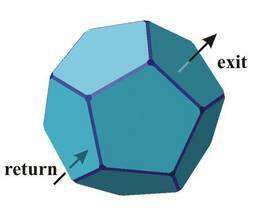
Un volume dont chaque point S de sa surface serait « identifié » (confondu) avec un point opposé E sur cette même surface, c’est à dire que toute trajectoire sortante en S serait au même instant une trajectoire entrante en E, est un espace multi-connexe. C’est par exemple le cas du volume d’une hypersphère ou d’un dodécaèdre de Poincaré. En effet dans ce type d’espace, toute boucle sortant/rentrant de la bordure du volume en S/E ne serait pas réductible en un point. Dans un tel espace tout rayon lumineux finit par revenir à son point de départ.

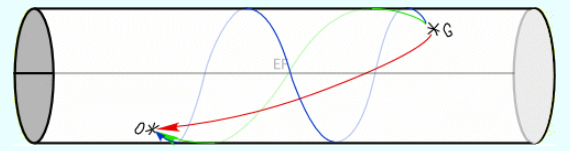
Il est à noter que dans un espace multi-connexe, les rayons lumineux, par exemple émis par une galaxie lointaine, pourraient nous parvenir par plusieurs trajets différents (cf les figures jointes d’un univers de Seyfert-Webber et d’un tube). Dans cette topologie, une même galaxie pourrait alors nous transmettre plusieurs images, d’aspects différents (taille, luminosité/éloignement, orientation), nous donnant ainsi l’illusion d’un nombre apparent de galaxies bien supérieur au nombre réel. Un peu comme si nous étions au milieu d’une pièce dont tous les murs, plafond et plancher étaient recouverts de miroirs. L’Univers pourrait donc également nous apparaître plus vaste qu’il n’est en réalité. Le schéma ci-contre montre une simulation de l’image d’une galaxie dans un univers multi-connexe (univers de Seyfert-Webber). Par illusion d’optique, on a l’impression d’être dans un espace multi-cellulaire constitué de plusieurs volumes géométriques collés les uns aux autres. Cet espace est un espace à courbure négative.

Une façon de savoir si nous sommes bien dans un univers multi-connexe est de s’intéresser au rayonnement fossile (CMB). En effet, la lumière se propageant en ligne droite et à vitesse constante, le rayonnement le plus lointain qu’on observe provient d’une région sphérique centrée sur nous, appelée « surface de dernière diffusion ». Si nous vivons dans un univers multi-connexe, alors tout se passe comme s’il y avait une infinité de copies de cette sphère dans l’univers. Si la distance entre ces sphères est inférieure à leur diamètre, alors en regardant le CMB, on devrait voir la même région émettrice dans plusieurs directions différentes. Ce sont en fait des paires de cercles dont on devrait trouver trace dans le rayonnement fossile, cercles présentant les mêmes motifs de température (cf schéma ci-contre). Ces paires de cercles pourraient cependant ne pas être parfaitement identiques car la lumière du rayonnement fossile peut avoir subi des altérations différentes en empruntant des trajets différents. <Sources : Alain Riazuelo>

Remarque sur la Relativité Générale :

La Relativité Générale traite d’un espace a priori connexe, et défini la gravitation comme une déformation géométrique de l’espace-temps. Elle ne prend pas en compte les diverses topologies possibles. Pourtant ces dernières ont un rôle capital dans la perception que nous avons de l’Univers.

Existe-t-il des univers parallèles ?

Toutes ces questions ont un point commun : elles suggèrent que l’espace et le temps que nous connaissons pourraient ne pas la seule et unique réalité.

La vidéo ci-contre (documentaire Arte) présente de façon très accessible la problématique des multivers.

La vision d’Aurélien Barrau sur le Multivers

Aurélien Barrau est astrophysicien et philosophe, Directeur du Centre de physique théorique Grenoble-Alpes. Il est notamment spécialiste de la Relativité Générale, des trous noirs et de cosmologie. Il mène également des recherches qui font référence sur la Gravité quantique à boucles.

Dans la conférence qu’il a donnée à l’Institut Physique Théorique du CEA (vidéo ci-contre), il expose sa vision du Multivers.

Jean-Pierre Luminet : un des meilleurs spécialistes de la forme de l’univers

L’un des plus éminents spécialistes de la forme de l’univers est l’astrophysicien français Jean-Pierre Luminet, Directeur de recherche au CNRS, Observatoire de Paris, Laboratoire d’Astrophysique de Marseille. 

Jean-Pierre Luminet a notamment travaillé sur les trous noirs super massifs, sur la forme de l’univers et plus récemment sur la Gravité quantique.

Ses recherches sur la forme de l’univers ont en particulier porté sur la topologie du dodécaèdre de Poincaré (PDS : Poincaré Dodecahedral Space) .

Dans la vidéo ci-contre, Jean Pierre Luminet fait état de ses recherches dans le domaine de la forme de l’univers.

La courbure de l’univers peut être déduite des propriétés du fond diffus cosmologique (CMB) cartographié avec une grande précision par le télescope spatial Planck en 2013. Premier verdict : la courbure serait très proche de zéro, à quelques millièmes près, en plus ou en moins, du fait de la marge d’erreur… Autrement dit, « quasi-euclidien ».

Cette hypothèse d’un univers « quasi-euclidien », à courbure nulle ou très faible, semble être partagée par une grande partie de la communauté scientifique.

Toutefois, une étude publiée dans la revue Nature en novembre 2019, et fondée sur une nouvelle interprétation des données du satellite Planck, indique cette fois une courbure positive « avec 99 % de probabilité ».  Selon Jean-Philippe Uzan, cosmologiste et Directeur de recherche au CNRS : « Ce résultat mérite confirmation. Mais l’idée d’un Univers sphérique n’est donc pas exclue. Quoi qu’il en soit, la théorie de l’inflation, qui décrit une augmentation exponentielle de la taille de l’Univers au moment du Big Bang, implique qu’à l’échelle de l’Univers observable, la courbure doit être très faible. Tout comme sur une sphère tellement dilatée qu’à sa surface, l’horizon semble plat ». Une telle faible courbure positive pourrait ainsi s’expliquer par la taille réduite de l’univers observable en regard d’un univers global dont nous ne connaissons pas la taille. Dans ce cas, seule la partie observable / « accessible » de notre univers présenterait une courbure nulle ou très faible dans un univers global dont la courbure pourrait être bien plus marquée. 

Un univers sphérique pourrait également expliquer quelques énigmes cosmologiques comme les disparités dans les mesures de la constante de Hubble.

Pour ce qui est de la topologie de l’univers, la recherche est également très active. Une équipe internationale de cosmologistes, conduite par Jean-Pierre Luminet, a en particulier étudié le modèle théorique multi-connexe de l’espace dodécaédrique de Poincaré pour expliquer certaines observations du rayonnement du fond cosmologique. Ce modèle d’univers s’appuie sur les données du satellite WMAP de la NASA (entre 2003 et 2006) qui ont fourni une carte à haute résolution du rayonnement du CMB. Au grandes échelles, ces données favorisent plutôt un espace fini, de courbure positive, et suggèrent une topologie multi-connexe. Ce modèle est cependant plus discuté depuis la parution des données du télescope spatial Planck (2009 à 2013), successeur de WMAP et plus précis.

Et pour conclure cette page en ouvrant sur quelques perspectives, je citerai Jean-Pierre Luminet :

« Avec la « cosmologie quantique », théorie à peine ébauchée et promise à de fascinants développements, se profilent des univers multiples, simultanés, sans interaction entre eux, ne différant les uns des autres que par leur géométrie, leur topologie, leurs constantes fondamentales de la physique.

Tous ces univers ne seraient que l’écume de l’Univers majuscule, lui infini et éternel, sorte d’océan bouillonnant, en transformation perpétuelle, que les physiciens appellent le « vide quantique ». On le voit, les enfants d’Héraclite n’ont pas dit leur dernier mot…« 

Δ  Ψ  Pour aller plus loin…

• « L’Univers chiffoné » de Jean-Pierre Luminet : Référence incontournable, cet ouvrage présente une exploration fascinante des différentes théories sur la forme de l’Univers, en s’appuyant sur les dernières découvertes scientifiques.
• « La réalité cachée » de Brian Greene : Ce livre nous guide à travers les concepts de la Théorie des Cordes et de la Mécanique Quantique dans un monde où les univers multiples et les dimensions supplémentaires pourraient nous aider à comprendre notre réalité.