Quelques fondamentaux théoriques
Distances et temps
Les notions de distance et de temps en astrophysique sont étroitement liées à la structure de l’espace-temps et à l’expansion de l’Univers (voir les pages « Mouvements et gravitation » et « Le destin de l’univers »).
Leur mesure est un défi majeur pour les astronomes, qui mettent en œuvre des méthodes de plus en plus sophistiquées pour sonder les profondeurs du cosmos.
Afin de mieux les appréhender, il est nécessaire d’introduire préalablement quelques concepts utiles :
L’espace-temps : un continuum indissociable
En astrophysique, les notions de distance et de temps ne sont pas aussi simples qu’elles peuvent le paraître à notre échelle. La Relativité Générale nous a appris que l’espace et le temps sont intimement liés et forment un continuum quadridimensionnel : l’espace-temps. Ce tissu cosmique peut être déformé par la présence de matière et d’énergie, ce qui a des conséquences directes sur la mesure des distances et des durées.
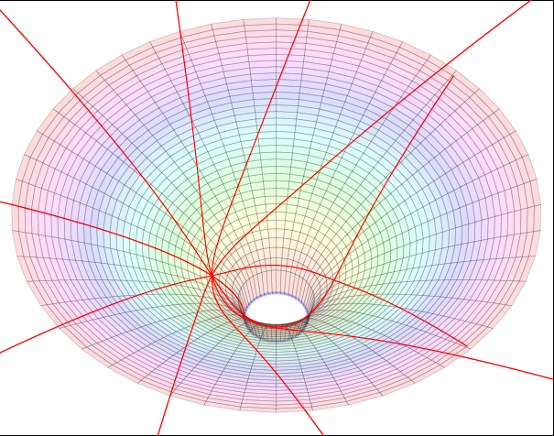
Les géodésiques : les chemins les plus courts dans l’espace-temps
Dans un espace-temps courbe, la trajectoire d’un objet, qu’il s’agisse d’une planète, d’une étoile ou d’un photon, est appelée géodésique. C’est le chemin le plus court entre deux points dans cet espace à quatre dimensions. Pour la lumière notamment, cela signifie que son trajet est dévié par la présence de masses, comme nous l’avons vu précédemment.
Les intervalles d’espace-temps
Pour caractériser les événements dans l’espace-temps, les physiciens utilisent la notion d’intervalle d’espace-temps. Cet intervalle peut être de type temps (séparant deux événements qui peuvent être reliés causalement), de type espace (séparant deux événements qui ne peuvent pas être reliés causalement) ou nul (séparant deux événements reliés par un rayon lumineux). La valeur de cet intervalle est invariante quel que soit le référentiel choisi, ce qui en fait une quantité fondamentale en Relativité Restreinte et Générale.
Le redshift cosmologique : une mesure de distance
Le redshift cosmologique est un décalage vers le rouge des raies spectrales des objets célestes lointains (cf la page « La lumière« ). Ce décalage est interprété comme une conséquence de l’expansion de l’Univers : plus une galaxie est lointaine, plus son redshift est élevé. Le redshift est donc utilisé comme une mesure de distance en cosmologie. Cependant, il faut noter que cette mesure est indirecte et qu’elle ne correspond pas à une distance « classique » dans un espace euclidien.
Le support théorique : la Relativité Générale
La notion d’espace-temps, un concept unifiant l’espace et le temps en une seule entité, est au cœur de la théorie de la Relativité Générale d’Einstein. Contrairement à la vision newtonienne d’un espace et d’un temps absolus, Einstein postule que l’espace-temps est dynamique et peut être courbé par la présence de matière et d’énergie. Cette courbure de l’espace-temps est en réalité la manifestation de la gravitation. Plus un objet est massif, plus il déforme l’espace-temps autour de lui, et plus les objets à proximité semblent « attirés » vers lui.
Voir également la page « Mouvements et gravitation ».
Validation par l’observation et l’expérience :
La Relativité Générale a été confirmée à maintes reprises par des observations et des expériences :
- La déviation de la lumière par le Soleil : Prédite par Einstein et confirmée lors de l’éclipse solaire de 1919, cette déviation de la trajectoire de la lumière par la masse du Soleil est une preuve directe de la courbure de l’espace-temps. (voir également la page « La lumière »)
- Les lentilles gravitationnelles : Lorsque la lumière d’une galaxie lointaine passe près d’un objet massif intermédiaire, son chemin est dévié, créant des images déformées ou multiples de la galaxie. Ce phénomène, appelé lentille gravitationnelle, est une conséquence directe de la courbure de l’espace-temps. (voir également la page « La lumière »)
- Les ondes gravitationnelles : Ces ondulations de l’espace-temps, prédites par la Relativité Générale, ont été détectées directement pour la première fois en 2015 par les interféromètres Ligo et Virgo. Elles sont produites par des événements cosmiques violents, comme la fusion de trous noirs.
- Le décalage vers le rouge gravitationnel (« décalage d’Einstein ») : La lumière émise par une source située dans un champ gravitationnel fort subit un décalage de son spectre électromagnétique vers les longueurs d’onde plus grandes (le rouge). Ce phénomène est dû à la dilatation du temps gravitationnel. (voir également la page « La lumière »)
Impacts sur notre perception de l’Univers :
La notion d’espace-temps a révolutionné notre compréhension de l’Univers :
- La gravitation comme une courbure de l’espace-temps : La Relativité Générale nous a donné une nouvelle vision de la gravitation, non plus comme une force agissant à distance, mais comme une manifestation de la géométrie de l’espace-temps.
- L’expansion de l’univers : La Relativité Générale a permis de comprendre l’expansion de l’univers, un phénomène découvert par Edwin Hubble dans les années 1920. (voir également les pages « La tension de Hubble » et « Le destin de l’univers »)
- Les trous noirs : La théorie prédit l’existence de régions de l’espace où la gravité est si intense que même la lumière ne peut s’en échapper : les trous noirs. (voir également la page « Les trous noirs »)
- Le Big Bang : La Relativité Générale, combinée avec les observations cosmologiques, suggère que l’univers a eu un début dans un état extrêmement dense et chaud : le Big Bang. (voir également la page « Du Big Bang à nos jours »)
En conclusion, l’espace-temps est un concept fondamental en astrophysique qui nous permet de comprendre les phénomènes cosmiques à grande échelle, de la formation des galaxies à l’évolution de l’Univers. Il nous offre une vision unifiée de l’espace, du temps et de la gravitation, et continue d’être au cœur de nombreuses recherches en astrophysique.
La notion de géodésique :
La géométrie euclidienne est celle de notre espace à trois dimension telle que nous le percevons à notre échelle (voir également la page « La forme de l’univers« ). Dans cette géométrie « usuelle » la géodésique est simplement la ligne droite, le chemin le plus court entre deux points.
Sur une sphère, espace à deux dimensions non euclidien, la géodésique est un grand cercle.
Mais plus généralement, mathématiquement, une géodésique est une courbe qui minimise la longueur d’arc entre deux points. L’équation d’une géodésique dépend de la métrique de l’espace, c’est-à-dire de la façon de mesurer les distances.
Les géodésiques dans l’espace-temps :
Comme nous l’avons vu, dans le cadre de la Relativité Générale, l’espace-temps est courbe en présence de masse et d’énergie. Les objets massifs déforment l’espace-temps, créant ainsi des « puits gravitationnels ». Une géodésique dans l’espace-temps est le chemin le plus court entre deux « événements », et non seulement entre deux points d’espace. Mais dans un espace-temps courbe, ce chemin n’est pas nécessairement une ligne droite. Physiquement, une particule libre (non soumise à d’autres forces que la gravité) suit une géodésique.
L’équation des géodésiques est une équation différentielle qui décrit la trajectoire d’une particule libre dans l’espace-temps. Elle dépend de la métrique de l’espace-temps, qui elle-même est déterminée par la distribution de masse et d’énergie.
La vidéo ci-dessus « Géodésiques et Relativité » d’Alessandro Roussel (ScienceClic) illustre ce concept de géodésiques dans un univers euclidien et dans l’espace-temps relativiste.
Implications astrophysiques :
Les géodésiques ont des implications profondes pour notre compréhension de l’univers :
- Orbites des planètes : Les planètes du système solaire suivent des géodésiques dans l’espace-temps courbe créé par le Soleil. Leur trajectoire elliptique est une conséquence directe de cette courbure de l’espace-temps.
- Lentilles gravitationnelles : La lumière suit également des géodésiques. Lorsqu’un objet massif se trouve entre une source lumineuse lointaine et un observateur, la lumière est déviée par la courbure de l’espace-temps, créant ainsi un effet de lentille gravitationnelle. (voir également la page « La lumière »)
- Trous noirs : Près d’un trou noir, l’espace-temps est tellement courbé qu’il n’y a pas de géodésiques sortantes au-delà de l’horizon des événements. Tout ce qui franchit cet horizon est piégé à l’intérieur du trou noir. (voir également la page « Les trous noirs »)
- Ondes gravitationnelles : Les ondes gravitationnelles sont des perturbations de la courbure de l’espace-temps qui se propagent à la vitesse de la lumière.
Elles sont générées par des événements cataclysmiques, comme la fusion de trous noirs. Le passage d’une onde gravitationnelle modifie localement la courbure de l’espace-temps. Par conséquent, les géodésiques, qui dépendent de cette courbure, sont elles aussi modifiées.
Les intervalles dans un espace euclidien :
Dans un espace euclidien, l’intervalle entre deux points est simplement la distance qui les sépare, calculée à l’aide du théorème de Pythagore. Cette distance est une propriété intrinsèque de l’espace et ne dépend pas du système de coordonnées choisi.
Les intervalles dans l’espace-temps :
En Relativité Générale, l’espace-temps est un continuum à quatre dimensions (trois spatiales et une temporelle) où la géométrie est courbe en présence de masse et d’énergie. De ce fait l’intervalle entre deux événements n’est plus simplement une distance spatiale, mais une quantité qui combine à la fois la distance spatiale et le temps qui sépare ces deux « événements ». Cet intervalle est appelé intervalle d’espace-temps.
La vidéo ci-contre « Intervalles espace-temps » (MinuteDePhysique) illustre ce concept d’intervalles.
pour « L’intervalle d’espace-temps est défini par l’équation de Minkowski :
ds² = -c²dt² + dx² + dy² + dz²où :
dsest l’intervalle d’espace-tempscest la vitesse de la lumière dans le videdtest l’intervalle de tempsdx,dy,dzsont les intervalles spatiaux
L’intervalle d’espace-temps peut être :
- de type « temps » si
ds² < 0: cela correspond à deux événements pouvant être reliés causalement (un événement peut influencer l’autre). Ce cas est possible lorsque les deux évènements sont spatialement suffisamment proches pour qu’un signal voyageant à une vitesse inférieure à celle de la lumière puisse les relier. - de type « espace » si
ds² > 0: cela correspond à deux événements trop éloignés spatialement pour être reliés causalement liés (aucun signal ne pourrait aller de l’un à l’autre sans dépasser la vitesse de la lumière). - nul si
ds² = 0: cela correspond à deux événements reliés par un rayon lumineux.
Implications en astrophysique :
Le concept d’intervalle d’espace-temps a des implications profondes en astrophysique :
- Dilatation du temps : Près d’un objet massif, le temps s’écoule plus lentement. Cela signifie qu’un intervalle de temps mesuré par un observateur proche d’un objet massif sera plus long qu’un intervalle de temps mesuré par un observateur loin de cet objet.
- Contraction des longueurs : Les longueurs sont également affectées par la gravitation. Un objet en mouvement par rapport à un observateur apparaîtra contracté dans la direction de son mouvement.
- Géodésiques : Les géodésiques, qui représentent les trajectoires les plus courtes dans l’espace-temps, sont déterminées par l’intervalle d’espace-temps.
- Trous noirs : Près d’un trou noir, l’espace-temps est tellement courbé que les intervalles d’espace-temps prennent des valeurs extrêmes, ce qui conduit à des phénomènes exotiques comme la dilatation infinie du temps à l’horizon des événements.
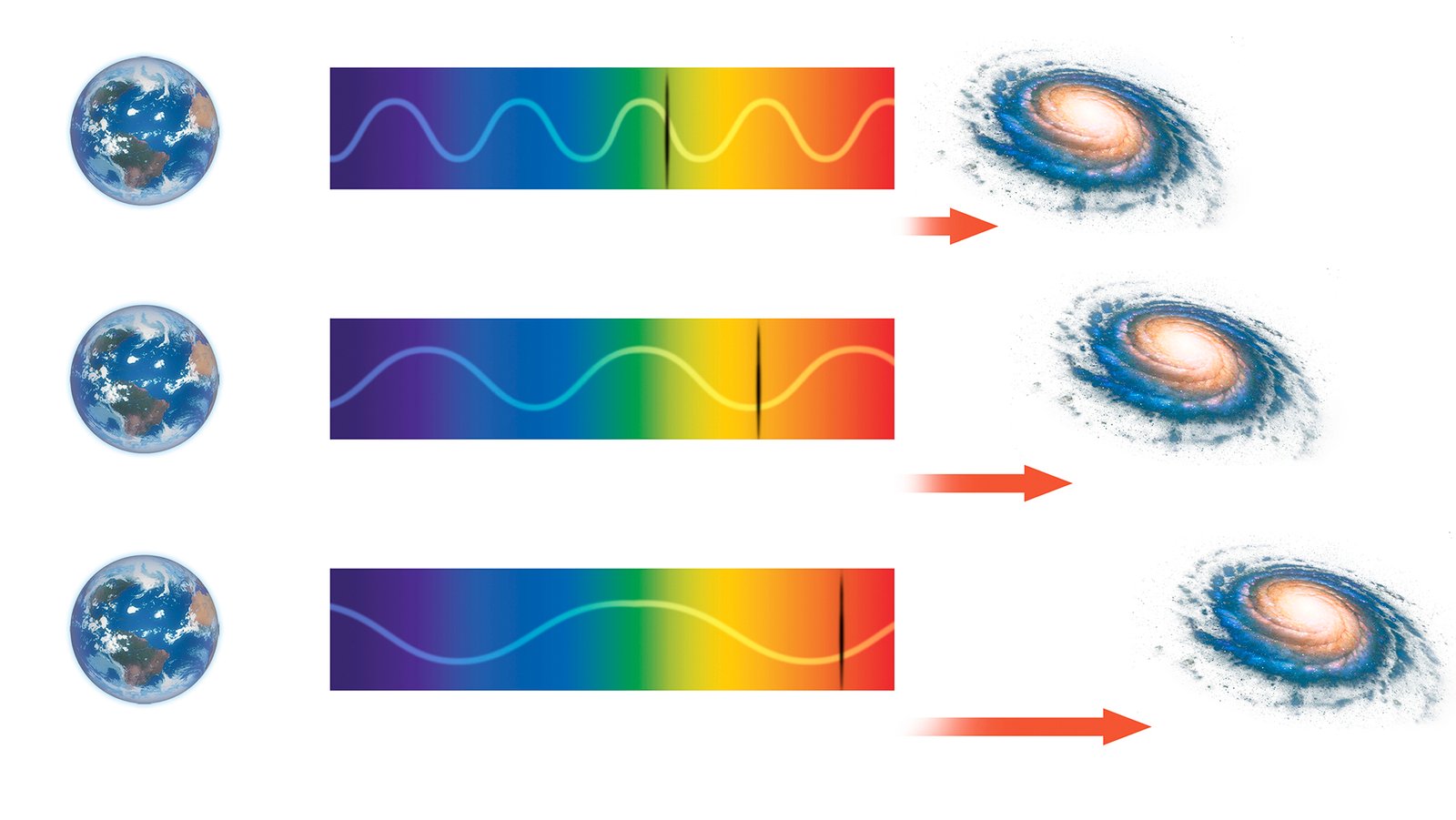
Qu’est-ce le redshift ?
Le redshift, ou décalage vers le rouge en français, est un phénomène astronomique observé dans le spectre lumineux des objets célestes lointains. Il se manifeste par un décalage des raies spectrales vers les longueurs d’onde plus grandes, c’est-à-dire vers le rouge du spectre visible.
Le redshift cosmologique est prédit par la théorie de la Relativité Générale d’Einstein et s’explique par l’étirement des longueurs d’onde de la lumière au cours de l’expansion de l’univers.
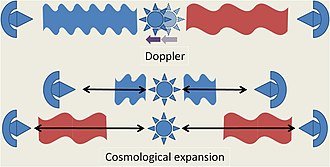
Le redshift cosmologique versus l’effet Doppler :
Il est important de ne pas confondre le redshift cosmologique avec l’effet Doppler. Bien que tous deux entraînent un décalage des fréquences, les causes sont différentes :
- Effet Doppler : Cet effet est dû au mouvement relatif de la source et de l’observateur. Si la source s’éloigne de l’observateur, les ondes sont « étirées » et la fréquence diminue, ce qui se traduit par un décalage vers le rouge.
- Redshift cosmologique : Ce phénomène est lié à l’expansion de l’Univers lui-même. L’espace entre les galaxies s’étire, ce qui entraîne un étirement des longueurs d’onde de la lumière qui les traverse.
Le support théorique :
Le redshift cosmologique est prédit par la théorie de la Relativité Générale d’Einstein et est décrit par la loi de Hubble-Lemaître :
v = H₀ × doù :
- v est la vitesse de récession de la galaxie (vitesse d’éloignement de l’observateur due à l’expansion de l’univers)
- H₀ est la constante de Hubble, qui représente le taux d’expansion de l’Univers
- d est la distance à la galaxie observée
Le redshift est quantifié par le paramètre z défini par :
z = (λ_observée - λ_émise) / λ_émise
où λ_observée est la longueur d’onde observée et λ_émise la longueur d’onde émise par la source.
Le redshift z est lié à la vitesse de récession par la relation approximative :
z ≈ v/coù c est la vitesse de la lumière.
Cependant, la relation entre redshift et distance n’est pas linéaire. Elle présente une courbure due à l’accélération de l’expansion de l’univers.
Voir également les pages « Le destin de l’univers » et « La tension de Hubble ».
Le redshift comme mesure de distance :
Le redshift est utilisé pour estimer la distance des objets célestes. Plus le redshift est élevé, plus l’objet est lointain. Cette méthode a permis de déterminer l’âge de l’Univers et de cartographier la distribution des galaxies.
Le redshift du Big Bang :
Le Big Bang étant considéré l’origine de l’expansion de l’univers, la lumière émise peu après cet événement aurait subi un redshift infini. Cependant, nous ne pouvons pas observer directement cette lumière, car elle est absorbée par le fond diffus cosmologique.
Les mesures récentes du télescope spatial James Webb :
Le télescope spatial James Webb, grâce à sa sensibilité dans l’infrarouge, permet d’observer des galaxies très lointaines, c’est-à-dire avec des redshifts très élevés. Les premières observations ont révélé des galaxies avec des redshifts supérieurs à 10, ce qui correspond à des distances de plusieurs milliards d’années-lumière.
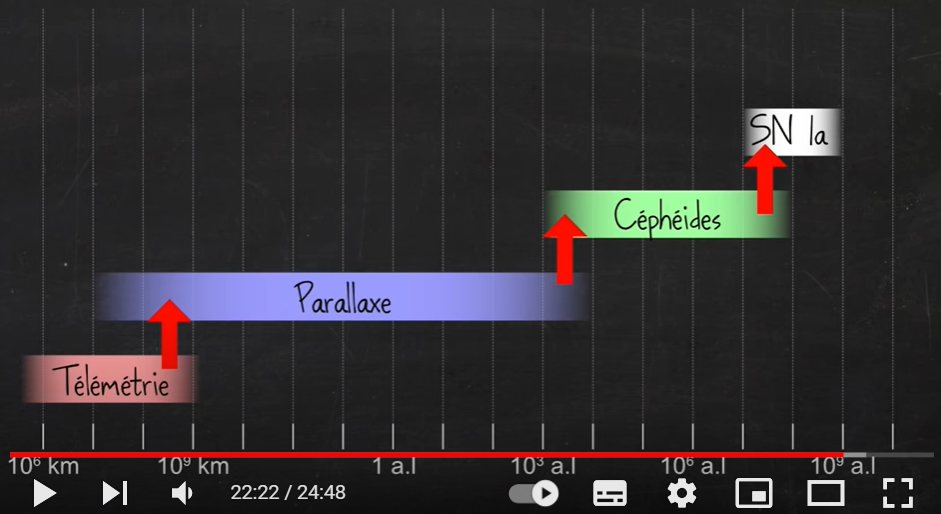
Mesurer des distances astronomiques est un défi de taille, mais essentiel pour comprendre l’Univers. Les astronomes ont développé diverses méthodes, chacune avec ses propres avantages et limites.
Les méthodes de mesure :
- Parallaxe trigonométrique : C’est la méthode la plus directe, mais limitée aux étoiles les plus proches. En observant le déplacement apparent d’une étoile par rapport aux étoiles plus lointaines au cours de l’orbite terrestre, on peut calculer sa distance. Cette méthode a permis de définir le parsec, une unité de distance astronomique qui équivaut à 3,26 année-lumière.
- Échelles de distance standard : Certaines étoiles, comme les Céphéides (étoiles qui varient de luminosité sur une période bien déterminée) ou les supernovae de type Ia (explosions stellaires extrêmement lumineuses), ont une luminosité intrinsèque bien connue. En comparant leur luminosité apparente à leur luminosité intrinsèque, on peut estimer leur distance. Ces étoiles servent également d’« échelles de distance » pour calibrer d’autres méthodes.
- Décalage vers le rouge : La loi de Hubble relie la vitesse d’éloignement d’une galaxie à sa distance. En mesurant le décalage vers le rouge de la lumière émise par une galaxie, on peut estimer sa distance. Cependant, cette méthode nécessite de connaître la constante de Hubble, qui est encore sujette à débat (voir la page « La tension de Hubble« ).
- Oscillations acoustiques baryoniques (BAO) : Ces oscillations, imprimées dans la distribution de la matière de l’Univers primordial, servent de « règle standard » pour mesurer des distances à très grande échelle.
La vidéo ci-dessus « Mesures de distances » de David Louapre (ScienceEtonnante) illustre les différentes méthodes de mesure des distances en astronomie.
Résultats récents :
- Le satellite Gaia a révolutionné la mesure des parallaxes, permettant de dresser une carte en 3D de notre galaxie avec une précision inégalée.
- Les supernovae de type Ia ont permis de mesurer avec précision l’accélération de l’expansion de l’Univers, révélant l’existence de l’énergie sombre.
- Les BAO ont confirmé l’homogénéité de l’Univers à grande échelle et ont permis de contraindre les paramètres cosmologiques.
Perspectives :
Les récentes missions spatiales en cours, comme les télescopes spatiaux James Webb et Euclid, devraient permettre d’affiner encore les mesures de distance et de mieux comprendre la nature de l’énergie sombre et de la matière noire. De nouvelles méthodes, comme celles utilisant les ondes gravitationnelles, pourraient également ouvrir de nouvelles perspectives.